Observe o seguinte problema:
Uma quadra de tênis tem a forma da figura, com perímetro de 64 m e área de 192 m2. Determine as medidas x e y indicadas na figura.
De acordo com os dados, podemos escrever:
8x + 4y = 64
2x . ( 2x + 2y) = 192 4x2 + 4xy = 192
Simplificando, obtemos:
2x + y = 16 1
x2 +xy = 48 2
Temos aí um sistema de equações do 2º grau, pois uma das equações é do 2º grau.
Podemos resolvê-lo pelo método a substituição:
Assim: 2x + y = 16 1
y = 16 - 2x
Substituindo y em 2 , temos:
x2 + x ( 16 - 2x) = 48
x 2 + 16x - 2x2 = 48
- x2 + 16x - 48 = 0 ->Multiplicando ambos os membros por -1.
x2 - 16x + 48 = 0
x'=4 e x''=12
Determinando y para cada um dos valores de x, obtemos:
y'=16 - 2 . 4 = 8
y''=16 - 2 . 12 = - 8
As soluções do sistema são os pares ordenados (4,8) e ( 12, -8).
desprezando o par ordenado que possui ordenada negativa, teremos para dimensões da quadra:
Comprimento =2x + 2y = 2.4 + 2.8 = 24m
Largura =2x = 2. 4 = 8m
Verifique agora a solução deste outro sistema:
Isolando y em 1
y - 3x = -1 y = 3x - 1
Substituindo em 2
x2 - 2x(3x - 1) = -3
x2 - 6x2 + 2x = -3
-5x2 + 2x + 3 = 0 ->Multiplicando ambos os membros por -1.
5x2 - 2x - 3 = 0
x'=1 e x''=-
Determinando y para cada um dos valores de x, obtemos:
Logo, temos para conjunto verdade:



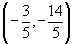

eu acho que essa poha ai ta errada.
ResponderExcluirreveja o que vc bota no blog.