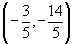O QUE É "PI" ???
"PI" é um número irracional, que não pode ser escrito como um número finito ou repetindo decimais. O valor aproximado é 3,1416 (lembrando que este não é seu valor exato, ele continua.).
Os egípcios sabiam trabalhar muito bem com as razões. Descobriram logo que a razão entre o comprimento de uma circunferência e seu diâmetro é a mesma para qualquer circunferência.
Por definição, " Pi " é a razão entre a circunferência de um círculo e seu diâmetro. " PI " será sempre o mesmo valor não importando o tamanho do círculo.
Matematicamente, escrevemos o número " PI " (p) como: comprimento da circunferência / diâmetro.
HISTÓRIA:
Os primeiros vestígios de uma estimativa de p , encontram-se do Papiro de Rhind escrito, aproximadamente, em 1700 a.C. , onde se lê : " a área de um circulo é igual a de um quadrado cujo lado é o diâmetro de círculo diminuído de sua nona parte".
Desde muito antes de Cristo, sabe-se que a razão C / D é constante. A procura desta constante foi tarefa árdua de grandes matemáticos ao longo da história.
Os gregos antigos já sabiam que a razão entre a circunferência (comprimento) de um círculo com o seu diâmetro resultava em uma constante ( que hoje chamamos de PI).
Por volta de 200 a.C. , o matemático Arquimedes de Siracusa aproximou PI inscrevendo polígonos em círculos e levando a relação da circunferência do polígono para o raio do círculo ( que também é o raio do polígono). Quanto mais lados no polígono, mais precisa a aproximação, foi a partir desta conclusão que Arquimedes escreveu um livro " A Medida de um Círculo". Neste livro, declara que PI é um número entre 3 10/71 e 3 1/7.O perímetro de uma roda de diâmetro 4 pés é dado por Vitruvius como sendo 121/2 pés, o que dá à PI o valor de 3 . 1/8. Essa aproximação não é tão boa quanto a de Arquimedes, cuja a obra Vitruvius provavelmente pouco conhecida, mas é de grau de precisão aceitável para as aplicações romanas.
Apolônio escreveu uma obra (agora perdida) chamada "Resultado Rápido" que pareceu ter tratado de processos rápidos de calcular p . Nela, diz-se que o autor obteve uma aproximação de p melhor do que a dada por Arquimedes. Provavelmente o valor que conhecemos com 3,1416. Não sabemos como foi obtido esse valor, que apareceu depois de Ptolomeu e na Índia. Na verdade, há mais perguntas não respondidas sobre Apolônio e sua obra do que sobre Euclides e Arquimedes, pois a maior parte de suas obras desapareceram.
Antes do tempo de Viéte havia já muitas aproximações boas e más para a razão da circunferência para o diâmetro de um círculo, tais como a de V.Otho e A.Anthonisk que, independentemente, redescobriram (por volta de 1573) a aproximação 355 / 113 , subtraindo numeradores e denominadores dos valores de Ptolomeu e Arquimedes, 377 / 120 e 22 / 7 respectivamente. Viéte calculou p corretamente a dez algarismos significativos, aparentemente sem conhecer a aproximação ainda melhor de Al- Kashi.
O uso do valor 3 para p na matemática chinesa antiga não chega a ser um argumento para afirmar dependência com relação à Mesopotâmia, especialmente porque a busca de valores mais precisos, desde os primeiros séculos da era cristã, era mais persistente na China que nos demais lugares. Valores como 3.1547 , , 92 / 29 e 142 / 45 são encontrados; e no terceiro século Liu Hui, um importante comendador do "Nove Capítulos", obteve 3.14 usando um polígono de 96 lados e a aproximação 3.14159 considerando um polígono de 3072 lados.
A fascinação dos chineses com o valor de p atingiu o ápice na obra de Tsu Chúng-Chisch (430-501). Um de seus valores era o familiar valor arquimediano 22 / 7, descrito por Tsu como "inexato", seu valor "preciso" era 355 / 113.
O inglês Willian Shanks calculou p com 707 algarismos exatos em 1873. Em 1947 descobriu-se que o cálculo de Shanks errava no 527º algarismo ( e portanto nos seguintes).
Com auxílio de uma pequena máquina manual, o valor de p foi, então calculado com 808 algarismos decimais exatos.
Depois vieram os computadores. Com seu auxílio, em 1967, na França, calculou-se p e, 500.000 algarismos decimais exatos e em 1984, nos Estados Unidos, com mais de dez milhões (precisamente 10.013.395) algarismos exatos.
Os motivos que levam as pessoas a se esforçarem tanto para calcular p com centenas ou milhares de algarismos decimais seriam: o "Livro dos Recordes de Guines"; e testes em computadores ( fazer as máquinas calcularem e comparar resultados).
POR QUE TAL NÚMERO É REPRESENTADO PELA LETRA GREGA p , QUE É EQUIVALENTE AO NOSSO " P " ?
Nos tempos antigos não havia uma notação padronizada para representar a razão entre a circunferência e o diâmetro. Euler, a princípio, usava ‘p’ ou ‘c’ mas, a partir de 1737, passou a adoptar sistematicamente o símbolo p . Desde então, todo o mundo o seguiu. Na verdade, alguns anos antes, o matemático inglês Willian Jones (1706) propusera a mesma notação, ou seja, utilizou a letra grega p para o número PI, sem muito êxito. Questão de prestígio.
POR QUE O CÍRCULO É DEFINIDO POR 360º ?
Grau é uma unidade de medida angular. Por convenção, a idéia de grau está diretamente relacionada como uma unidade que mede ângulos, assim como o metro mede duração, grama mede massa, segundo mede tempo,...
Além do grau, temos outra unidade para medir arcos e ângulos que é o radiano.
Considerando um arco , contido numa circunferência de raio R, tal que o comprimento do arco seja igual a R..
Um radiano ( 1 rad. ) é um arco cujo comprimento é igual ao do raio da circunferência que o contém.
O angulo AOB mede 1 rad. se, e somente se, determine numa circunferência de centro O um arco de 1 rad.
SE A MEDIDA DA CIRCUNFERÊNCIA É 360º. QUAL SERÁ A MEDIDA EM RADIANOS?
O comprimento de uma circunferência de raio R, numa certa unidade U, é dado por 2p R, pois se .
Temos 2R igual ao diâmetro, aplicando meios por extremos obteremos: C= 2p R ou seja, o comprimento da circunferência.
Logo, sendo X a medida da circunferência em radianos, temos:
Rad. U
1 ____________ R
X ____________ 2p R
\ X= rad.
X = 2p rad. .......... medida da circunferência em radianos.
Como definição temos que uma medida a graus é equivalente a outra medida b radianos se, e somente se:
a º / 360º = b rad. / 2p rad.
( se forem medidas do mesmo arco)
Esta equivalência nos permite transformar unidades de graus para radianos e vice-versa.
FACILITANDO CÁLCULOS
O número p surge inesperadamente em várias situações. Por exemplo, Leibniz notou que 1 – 1 / 3 + 1 / 5 – 1 / 7 + ... = p/ 4 e Euler provou que a soma dos inversos dos quadrados de todos os números naturais é igual a p2 / 6. A área da região plana compreendida entre o eixo das abcissas e o gráfico da função é igual a . Inúmeros outros exemplos poderiam ser mencionados, como o seguinte: a probabilidade para que dois número naturais, escolhidos ao acaso sejam primos entre si é de 6/p2.
Como podemos observar o número p serve para tornar mais acessíveis alguns cálculos.
Um número fascinante
PI, o valor da razão entre a circunferência de qualquer círculo e seu diâmetro, é a mais antiga constante matemática que se conhece. E' também um dos poucos objetos matemáticos que, ao ser mencionado, produz reconhecimento e ate mesmo interesse em praticamente qualquer pessoa alfabetizada.
Apesar da antiguidade do nosso conhecimento do PI, ele ainda é fonte de pesquisas em diversas áreas. Com efeito, dentre os objetos matemáticos estudados pelos antigos gregos, há mais de 2 000 anos, Pi é um dos poucos que ainda continua sendo pesquisado: suas propriedades continuam a ser investigadas e procura-se inventar novos e mais poderosos métodos para calcular seu valor, sendo que a divulgação desses resultados constitui uma das raras ocasiões em que vemos a Matemática atingindo os meios de comunicação de massa.
Como uma conseqüência dessa situação, e como uma outra maneira de demonstrar o interesse e fascinação despertados pelo PI, os editores estão sempre a publicar livros dedicados inteiramente ao tema e dirigidos tanto ao grande público como a professores e pesquisadores. Entre os mais recentes, podemos destacar:
- Lennart Berggren (ed) - Pi: A Source Book
Springer Verlag, 2nd ed., NYork, 2000
( nada menos do que 736 paginas! )
- J. P. Delahaye - Le fascinant nombre Pi
Editions Belin / Pour La Science, Paris, 1997.
- J. Arndt - PI, unleashed.
Springer Verlag, NYork, 2000.
Os vários tipos de PI
Em verdade, na Geometria Euclidiana, temos quatro constantes que poderiam ser chamadas de PI:
- PI de circunferências: a constante de proporcionalidade na relação entre a circunferência de um círculo e seu diâmetro
- PI de áreas de círculos: a constante de proporcionalidade na relação entre a área de um círculo e o quadrado de seu diâmetro
- PI de áreas de esferas: a constante de proporcionalidade na relação entre a área de uma esfera e o quadrado de seu diâmetro
- PI de volumes de esferas: a constante de proporcionalidade na relação entre o volume de uma esfera e o cubo de seu diâmetro
Usando as fórmulas clássicas da Geometria, fica muito fácil expressarmos qualquer uma dessas constantes de proporcionalidade em termos das demais. Por questão de tradição, prefere-se trabalhar exclusivamente com o PI da circunferência de círculos, o qual é denotado internacionalmente pela letra pi minúsculo, a letra inicial da palavra grega peripheria que significa perímetro ou circunferência ( essa notação surgiu no início do sec. 1700 e foi adotada e popularizada pelo importante livro Análise Infinitesimal, escrito por Euler c. 1750 ).
A descoberta do PI
Muitas pessoas acham que precisamos ter o valor do PI para calcular circunferência de círculos. Um exemplo clássico mostrando que isso NAO e' verdade e' o cálculo da circunferência da Terra por Erathostenes c. 250 AC. Ele mediu um arco de meridiano terrestre de 5000 estádios e, usando um instrumento de forma semi-esférica ( chamado skaphe ), verificou que esse arco de meridiano era proporcional a um arco de meridiano da skaphe, o qual media 1/50 do meridiano da esfera desse instrumento. Conseqüentemente, concluiu que o meridiano terrestre e' 50*5000 = 250000 estádios. Ou seja, em lugar nenhum precisou saber o valor do PI!
Esse exemplo, e outros que poderíamos mencionar, mostram que é bastante surpreendente que a quase totalidade das pessoas ache que PI foi descoberto ao se relacionar circunferências com diâmetros dos respectivos círculos. Embora a definição usual do PI baseie-se na constância da razão circunferência : diâmetro, muito provavelmente não foi essa a origem do PI. Com efeito, é difícil imaginarmos situações práticas reais onde, numa civilização incipiente, alguém tenha precisado calcular a circunferência de um círculo de diâmetro conhecido, ou vice-versa. Muito mais naturais são problemas requerendo achar a área de um campo circular em termos do diâmetro ou mesmo em termos da circunferência. Em verdade, devia-se até questionar se a descoberta do PI realmente ocorreu no contexto de círculos, e não no de esferas.
Essa inquietação não é só nossa. O famoso historiador matemático Abraham Seidenberg gastou muitos anos de sua vida vasculhando museus e lendo trabalhos de antropologia, em busca dos mais antigos indícios de envolvimento humano com círculos, esferas e o PI. O resultado desses estudos foi resumido nos seus artigos The ritual origin of the circle and square, Archiv. Hist. Exact Sc. 25, (1981), e principalmente em On the volume of a sphere, Archiv. Hist. Exact Sc. 39, (1988). Sua conclusão foi que o cálculo do volume da esfera em termos de seu diâmetro remontaria a antes de 2 000AC, sendo anterior a matemática das grandes antigas civilizações mesopotâmicas, indiana, chinesa e egípcia. O historiador matemático B. van der Waerden identifica essa origem com o que chamo de Tradição Origem da Matemática e a localiza no Vale do Danúbio c. 4 000 AC. Segundo Seidenberg, nessa tradição também se teria reconhecido a igualdade da constante de proporcionalidade relacionando circunferência com diâmetro e área de círculo com quadrado do raio; ou seja, já nessa tradição, possivelmente lá por 3000 a 4000AC, se teria reconhecido que o "PI da circunferência" é igual ao "PI da área do círculo". Também é interessante observar que Seidenberg concluiu que a descoberta dessa igualdade usou métodos infinitesimais, ao estilo de Cavalieri.
É preciso que fique bem claro que o que o trabalho de Seidenberg achou na noite dos tempos, em bem remota antiguidade, foram apenas indícios indiretos de envolvimento com PI. Os mais antigos documentos concretos que temos e que tratam explícitamente de PI são tabletas mesopotâmicas de c. 2 000 AC, como a mostrada ao lado. Examinando a figura desenhada, fica fácil ver que a mesma corresponde a adotar a aproximação grosseira PI = 3, que é a mais comum das aproximações para PI que encontramos nos documentos mesopotâmicos.
Por que é tão difícil calcular o PI?
A principal razão é que PI não é uma fração. Com efeito, se PI pudesse ser escrito como uma fração m / n, seu cálculo poderia
- ou se resumir em buscar o valor de tais numeros inteiros m e n
- ou explorar a periodicidade de sua representação decimal
( por exemplo, se fosse verdade que PI = 22 / 7 = 3.142857 142857 142857 ..., então nos bastaria achar o valor da parte inteira, 3, e o bloco 142857 que se repete indefinidamente )
O fato de que, por mais de 2000 anos, ninguém tivesse conseguido explorar nenhuma das duas possibilidades acima é exatamente o que sugeriu que PI não deva ser uma fração. A verificação rigorosa desse fato, ou seja a demonstração da irracionalidade de PI, veio só com Lambert, em 1 761.
Em verdade, por si só, a irracionalidade de PI não seria suficiente para determinar a dificuldade de seu cálculo; com efeito, existem irracionais de representação decimal previsível, e então fáceis de calcular, como é o caso de 3.10110111011110... . PI é difícil de calcular porque é um irracional imprevisível: sua representação decimal não mostra nenhuma previsibilidade, sendo que acredita-se que seus algarismos se distribuam aleatoriamente.